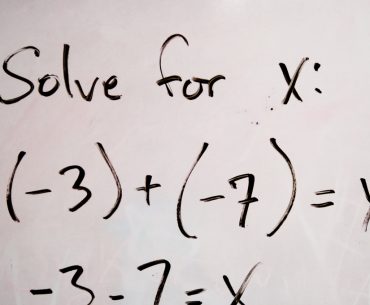In daily life we use mathematics to estimate our budget, calculate price, profit, loss etc. Doing this work is…
Last Friday, my family adopted a sweet, little poodle puppy, named Zipper. The foster mother, Sally, had brought him…
If there’s one thing most folks assume about me, it’s this: That I am some sort of mathmagician, able to…
If you’re on Facebook, you’ve probably seen one of a variety of graphics like the one above. The idea is…
In redesigning my blog, I’ve read a lot of the posts I’ve written over the last year. In fact,…
Photo courtesy of .raindrops. Every so often, at around 7:00 p.m., I’ll get a call from someone I know.…
Photo courtesy of .raindrops It’s the No. 1 question asked of math teachers: “When will I ever use this…
Photo courtesy of woodleywonderworks. All summer long, we’ve seen some pretty amazing research on math ability and education. We’ve…
Bon Crowder, another math evangelist Bon Crowder, another math evangelist couple of weeks ago, a fellow freelance writer wrote…
When I was a camp counselor after my sophomore year of college, I had a standard response to kids…
I’m on the right track, babyI was born this way–Lady Gaga It was day two of my second year…